再谈归并排序
在我以前的资料结构专栏中已经对归并排序做了介绍,这里我们开始先复习一下归并排序的思路与代码
归并排序用到了分治的思想,将阵列不断细分成小的几个区间,将每个区间排成有序后,再将大区间排为有序
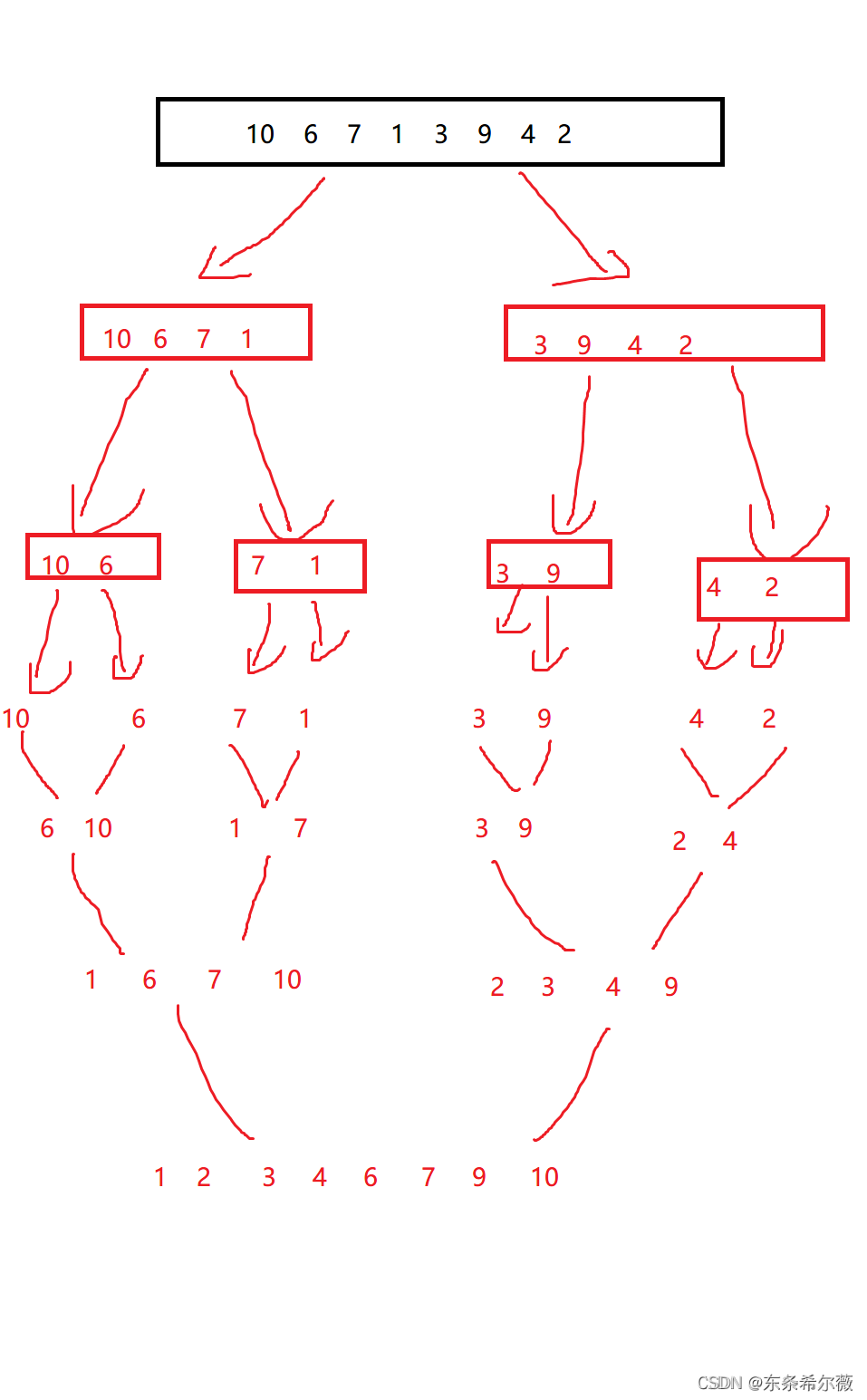
代码实作:(非递回实作)
void _MergeSort(vector<int>&arr,int l,int m,int r);//归并操作的函式
void MergeSort(vector<int>&arr)
{
int n=arr.size();
int gap=1;//每次归并的小区间
while(gap<n)
{
int l=0;
while(l<n)
{
int m=l+gap-1;//左区间的末尾
if(m>=n)
{
break;//左区间不存在(没有对应的右区间),直接不进行归并
}
int r=min(n-1,m+gap);//判断右区间是否越界,右区间不够其实可以继续归并
_MergeSort(arr,l,m,r);//进行归并操作的函式
l=r+1;//归并完后继续更新下一个区间
}
if(gap>n/2)
{
break;//防止溢位
}
gap<<=1;//每次将gap*2,扩大区间
}
}
void _MergeSort(vector<int>&arr,int l,int m,int r)
{
int help=(int*)malloc(sizeof(int)*(r-l+1));//归并辅助阵列
int p1=l;
int p2=m+1;
while (p1 <= m && p2 <= r)
{
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m)
{
help[i++] = arr[p1++];
}
while (p2 <= r)
{
help[i++] = arr[p2++];
}
for (i = 0; i < (r - l + 1); i++)
{
arr[l + i] = help[i];
}
free(help);
}
小和问题
问题描述
有一个阵列arr,设有一个指标i指向某一个元素,将i左边所有比i小的数字加起来求和,将i遍历整个阵列求出最终答案
图例
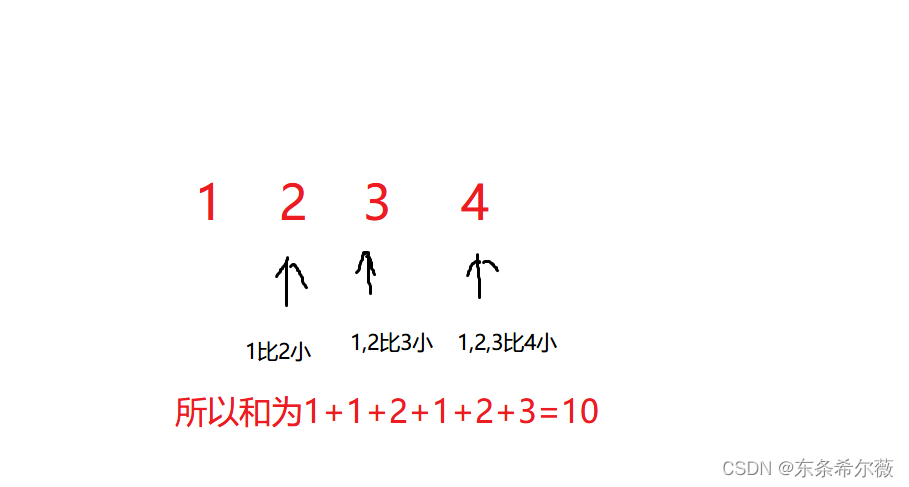
思路
我们可以直接用暴力的方法,用两个指标遍历来找小数,当然,不是不可以,但是复杂度是O(n2)我们一般不考虑,下面介绍一种转化方法
我们可以把问题转化为求右边有多少个数比i大
比如在上面这个阵列
1比2,3,4都大,所以2,3,4在算的时候一定会加一个1,所以我们可以在遍历1的时候加上1*右边有多少个数比1大
但是我们拿到的阵列不一定有序,就像这样
[2,3,5,4,6,8,9,7];
所以我们需要排序来完成,因为排序完再算复杂度较高,所以我们可以边排序边计算
在归并的时候可以一个区间区间的计算
在归并到右区间的时候不计算的,归并左区间时计算右区间有多少数比它大,答案加上右区间长度*这个数本身
相等时归并右区间:相等归并左区间右区间究竟大还是小不清楚
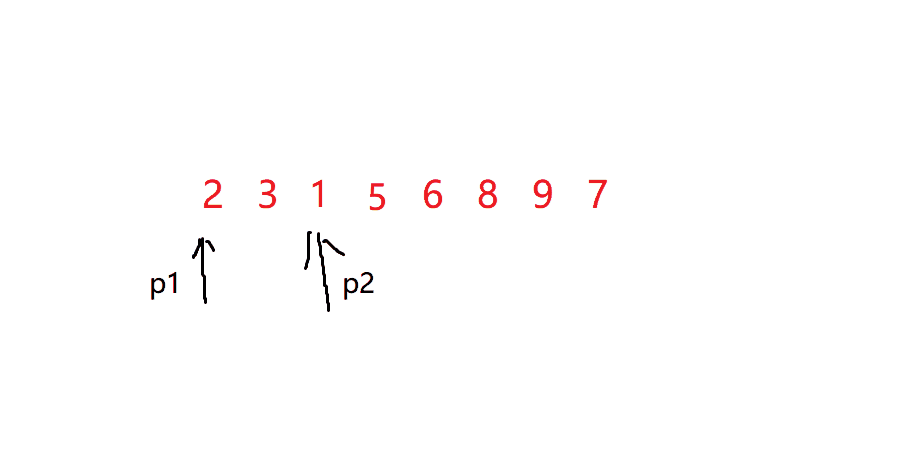
代码实作
int Process1(vector<int>& arr, int l, int m, int r)
{
int ans = 0;
int* help = (int*)malloc(sizeof(int) * (r - l + 1));
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
ans += arr[p1] < arr[p2] ? (arr[p1] * (r - p2 + 1)) : 0;//对答案进行操作
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < (r - l + 1); i++) {
arr[l + i] = help[i];
}
free(help);
return ans;
}
int smallSum(vector<int>& arr,int l,int r)
{
if (l == r)
{
return 0;
}
int mid = l + ((r - l) >> 1);
return smallSum(arr, l, mid) + smallSum(arr, mid + 1, r) + Process1(arr, l, mid, r);//process是归并函式
}
逆序对问题
我们把(x,y)二元组叫做一个对,逆序对满足右边的数字比左边小
给你一个阵列,判断它有多少个逆序对
思路求解
与上一题差不多,但这题我们从右往左归并,我们转化为数右区间有多少个数比左区间小即可
如果从左往右归并的话,我们就不能确定右区间比左区间大了,也不能确定有序
int Process2(vector<int>& arr, int l, int m, int r)
{
int ans = 0;
int* help = (int*)malloc(sizeof(int) * (r - l + 1));
int i = (r - l + 1) - 1;
int p1 = m;
int p2 = r;
while (p1 >= l && p2 > m) {
ans += arr[p1] > arr[p2] ? (p2 - m) : 0;
help[i--] = arr[p1] > arr[p2] ? arr[p1--] : arr[p2--];
}
while (p1 >= l) {
help[i--] = arr[p1--];
}
while (p2 > m) {
help[i--] = arr[p2--];
}
for (i = 0; i < (r - l + 1); i++) {
arr[l + i] = help[i];
}
free(help);
return ans;
}
int reverPairNumber(vector<int>& arr, int l, int r)
{
if (l == r)
{
return 0;
}
int mid = l + ((r - l) >> 1);
return reverPairNumber(arr, l, mid) + reverPairNumber(arr, mid + 1, r) + Process2(arr, l, mid, r);
}












0 评论